Numerical Playfair by Zag
Puzzle solution process
This is one possible solution path.
As 9ac is the Playfair code-number, we know that the code-square consists of that two-digit number followed by the other seven digits in ascending order. As the digits of 9ac are the first and second in the top row of the square, its encoded form is the second and third digits in the same row, so the second digit of the grid entry is the one from the top-right corner of the code-square. This can only be one of {1, 2, 3} (because there are only six digits from 4 to 9, not enough to fill the seven non-code-number places in the code-square); but the same grid cell is the end of 6dn which is a square, so it can only be 1.
So 6dn is the square of a number ending in 1 or 9, ie one of {121, 361, 441, 841, 961}, which means that 7ac ends in one of {2, 4, 6}. As 3dn is a multiple of 7ac, it must also be even. It’s the reverse of 2ac, so they both have the same middle digit, but the middle digit of 2ac shares the same cell as the first of 3dn, so 2ac is of the form xyy and 3dn is yyx, with x being one of {2, 4, 6, 8} (not 0, which isn’t allowed at the start of 2ac). The ratio of 3dn/7ac can’t be 1 (or the two entries would be the same) or 5 (which would make 3dn end in 0) or >9 (as both numbers have three digits), so it’s one of {2, 3, 4, 6, 7, 8, 9}.
If the ratio is 2, 7ac ending in {2, 4, 6} means 3dn ends in {4, 8, 2} respectively, so 7ac ends in {42, 84, 26}, then 3dn ends in {84, 68, 52}, ie 3dn would be {884, 668, 552} and 7ac would be {442, 334, 276}; of these, 884/442 would fit for 3dn/7ac, but the others would make the last digit of 3dn clash with the second digit of 7ac. Similarly, if the ratio is 3 then 3dn ends in {6, 2, 8}, 7ac ends in {62, 24, 86}, 3dn is {886, 772, 558} and 7ac is {295.3, 257.3, 186}, of which only 558/186 is valid. If the ratio is 4, the values for 7ac come out as {57, 139, 221}, all odd; if the ratio is 6, the only integer values are 996/166; if the ratio is 7, we get 994/142 and 882/126; if the ratio is 8, we get 992/124; if the ratio is 9, none of the values for 7ac is an integer. For 7ac’s candidate values {442, 186, 166, 142, 126, 124}, the corresponding digit sums for 2dn are {10, 15, 13, 7, 9, 7}, but 2dn has to be a two-digit number without 0, so we’re limited to {186, 166} for 7ac, with 3dn being {558, 996} respectively.
We know 7ac ends in 6, so 6dn is one of {361, 961} and 5dn has the same digits. Neither 4ac nor 8ac can have a 1 in the middle, because the code-square has 1 in the top-right corner, not in the middle of any row or column; therefore 1 has to be the middle digit of 5dn. In the code-square, the 9 can be either in one of the first two cells (part of the code-number) or in the last cell, ie not in the middle row, so the middle digit of 8ac can’t be 9. Thus 5dn is one of {316, 613, 916} and 6 is in the middle of either a row (4ac) or a column (8ac) of the code-square.
If 7ac is 166 then 3dn is 996, 2ac is 699 and 2dn is 13 encoding to 6_. For 1 to encode to 6, they must be in the same row or column of the code-square, ie either the top row or the right-hand column. If they’re in the same column, it has to be 163 to encode 13 to 6_ (specifically, 61), but then the digits at the bottom of the code-square wouldn’t be in ascending order. Having 6 in the top row (in the middle, as above) would give _61 for 4ac, so the grid entry for 2dn would be 61, but encoding 13 to 61 would require the top row to be 631 (or 316 or 163), not _61. So 7ac isn’t 166.
Therefore, 7ac = 186, 3dn = 558,
2ac = 855 and 2dn = 15 entered as 8_.
In the code-square the 5 can’t be in the last column,
because a column of 15_ would encode 15 to 5_ instead of 8_,
and the bottom-right corner can only have one of {7, 8, 9}.
If the 5 is in the top row
then it can’t be 5_1 (which would encode 15 to 5_),
so it has to be 851, encoding 15 to 81 for 2dn,
and 4ac is the 851 row;
but the middle digit of 4ac can’t be 5,
so that’s impossible.
If the 5 is at the start of the middle row
then the omitted {2, 3, 4} all have to be used in the code-number;
if it’s second in the middle row
then 8 is above it in the top row (so 15 encodes to 8_),
but two out of {2, 3, 4} have to be used in the code-number _8;
if it’s in the middle of the bottom row
then three of {6, 7, 8, 9} have to be used in the code-number.
Therefore 5 is in the bottom-left corner of the code-square,
8 is in the top-left corner
and 4ac is the bottom row.
Now the middle digit of 4ac can’t be 3 or 9,
because 53_ or 59_ for the bottom row wouldn’t have
all of its digits in ascending order,
so 4ac is 56_, 5dn = 613
and 6dn = 361.
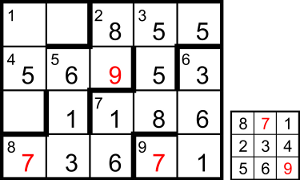
What we know of the code-square is now [8_1, 234, 56_],
so 8ac is the middle column, _36.
The two possibilities for the grid and code-square so far are shown here.
Both give a prime for 7dn, either 79 or 97 encoding to 16.
One of the entries is a factor of 855,
which is easily factorised as 3×3×5×19,
its non-trivial factors with two or three digits being
{15, 19, 45, 57, 95, 171, 285}.
Neither of the three-digit factors fits in either grid,
and the only place for any of the others is 1ac.
If 1ac is 95 then 1ac + 1dn is in the range [1045, 1054]
but there are no squares in that range;
if 1ac is 57 then 1ac + 1dn is in the range [607, 616]
with no squares;
if 1ac is 45 then 1ac + 1dn is in the range [495, 504],
again with no squares;
for the other two factors, the only square within range is 169,
so the sum is either 15 + 154 or 19 + 150.
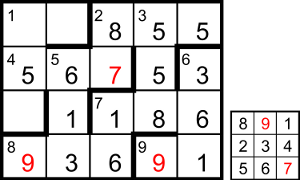
Including the 1 at the start of 1ac, the sum of digits in the first grid so far is 87, and the remaining two cells will sum to 9 (either 5 + 4 or 9 + 0), so the grid total is 96; but for that grid 96 would encode to 59, not 15 or 19. For the second grid, the sum of digits so far is 89, so the grid total is 98, which encodes to 19. Therefore 1ac = 98 encoded to 19, 1dn = 150, 4ac = 567, 2dn = 87, 8ac = 936, 9ac = 91 and the grid is complete.
