Pentominoes by Child’s Play
Puzzle solution process
This is one possible solving path. The first 13 primes are {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41}. For convenience, we’ll label the grid’s columns a to g and the rows 1 (top) to 7, so cells can be referred to by column-row coordinates, from a1 to g7. There are 45 white cells in the grid, so the sets of five each of the digits 1 to 9 must fill all of them, with no zeroes anywhere. There are 12 pentomino shapes, which are conventionally referred to by letters that they resemble, as shown here.

F
I
L
N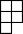
P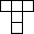
T
U
V
W
X
Y
Z
Starting with the 7ac clue C(HC), C can’t be as big as 5 because the minimum for H5 would be 25 = 32 and 56 = 15625 is already too big for the four-digit answer. If C is 2, the first possibilities for H give 2(32) = 512 and 2(52) = 33554432, both of the wrong length. So C = 3. H can’t be as big as 5 because 3(53) is clearly > 2(52), so H = 2 and the answer to clue 7ac = 6561. The only pentomino that could connect the two 6s is the U pentomino. If 6561 were entered across from cell a1 or d7, the U would be blocked by a black cell; starting in a5, the U could join the 6s by going up into row 4, but then the 5 in b5 would be isolated and unable to form a pentomino. Therefore 6561 goes from d3 to g3, with the U completed by three 6s in row 4.
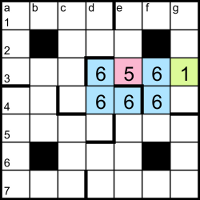
Now the 5 pentomino needs to take the e2 cell above; it can’t take d2 because that would make the down entry end in 5 and the clues say that both two-digit down entries are primes, so the pentomino extends up to e1. It can’t extend right as far as g1 because that would make two grid entries the same, 555, so it must take at least one cell to the left (d1). The only other digit that can reach g1 is 1, so the top three cells in column g are part of the 1 pentomino.
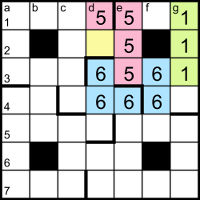
Cell f1 can only contain 1 or 5. If it’s 1 then the 1s form an L pentomino and the 5s are forced into a V pentomino, taking c1. Then the top-left corner cells {b1, a1, a2, a3} would be part of a new pentomino, but its fifth cell would make it either a U or an L, duplicating one of the existing shapes. So f1 is 5 and the 5s form a T pentomino. Now the 1s can only form an I pentomino. Cells in the bottom-right corner are now isolated and must form an L, in order to avoid becoming a second U.
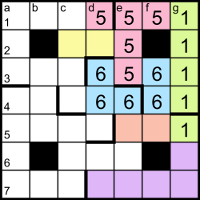
The two entries containing 66_ in columns d and f must be different, so cell d5 must contain a different digit from f5 and the pentomino starting in f5 must zigzag to form an N pentomino. Now cells in the bottom-left corner are isolated and can only form a V pentomino.
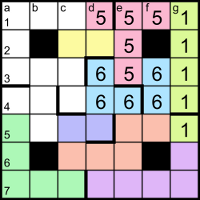
If the digits in cells a1 and b1 are the same then the only pentominoes they can form are an N (with the yellow cells c2 and c3), a V or an L, all of which would be duplicates of existing shapes; therefore they must belong to different pentominoes. Cell b1 can now only join with the yellow cells, forming an F pentomino. To avoid forming another V, N or L, the cells down from a1 must make an upside-down Y pentomino. And the remaining cells are left to form a P pentomino, completing the partitioning of the grid.
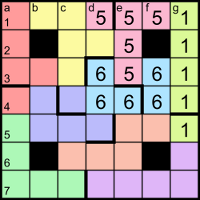
The answers to the down clues GKL − 3 and GKL + 3 have three digits, so GKL must be a three-digit number; if none of {G, K, L} is 5 then the minimum for the product is 7×11×13 = 1001, too big. Therefore GKL ends in 5, GKL − 3 ends in 2 and GKL + 3 ends in 8, and the entries for GKL ± 3 must have the same first two digits. From the grid colouring, we can see that the only such entries are the ones starting with 66, so the P and N pentominoes are composed of 2 and 8, but we don’t yet know which is which. We do know GKL = 665, so {G, K, L} = {5, 7, 19}. The 5dn clue says KL has three digits, so it must be 7×19 = 133, with G = 5. The only available 1 in the grid for KL = 133 is at the bottom of column g, so the L pentomino is composed of 3s.
Clue 4ac says CHM = 6M has three digits, and from the grid we know it doesn’t start with 1 or 6; in fact, apart from the central _66, all the three-digit across entries have either the first two or all three digits the same. M is at least 221/6 ≈ 36.8, ie one of {37, 41}, but 6×41 = 246 doesn’t have the right digit pattern, so M = 37 and 4ac = 222. We know that the 2s are in either the P pentomino or the N, and the only three-digit across entry therein is the one in row 6, which allows us to place all the 2s and 8s.
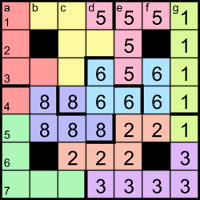
Clue 5ac says JK has three digits. If K is 7 then J is at least 221/7 ≈ 31.6, ie 41 (because 37 is already taken by M), but 7×41 = 287, which doesn’t have the right digit pattern. Therefore K = 19 and L = 7.
Clue 6ac says ACDG = 15AD has four digits. As it’s a multiple of 5 and can’t end in 0, it must end in 5 and be entered across from cell a1. The unknown digits are from {4, 7, 9}. It’s a multiple of 3, so the sum of its digits must be divisible by 3. If it starts with 4, the middle two digits must therefore be 99, but the digit sum of 4995 is 27, which makes it a multiple of 9, and only one 3 is allowed among its prime factors. If it starts with 9, neither 9445 nor 9775 has a digit sum divisible by 3. So it starts with 7 and to be a multiple of 3 it must be 6ac = 7995 = 3×5×13×41. Now we can place all the remaining digits in the grid.
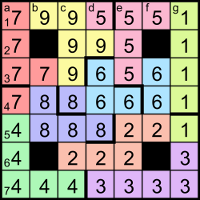
For completeness, we can resolve the remaining variables, though we don’t need them to finish the grid. From 6ac, we know {A, D} = {13, 41}. For clue 5ac, JK = 19J must be one of the odd across entries {551, 995, 779, 221}; of those, the only multiples of 19 are 551 = 19×29 and 779 = 19×41, but 41 is already taken (by either A or D), so J = 29 and 5ac = 551.
For clue 3ac, BD must be one of the remaining odd across entries {995, 779, 221} and it’s divisible by D, which is either 13 or 41. 995 isn’t divisible by either of those and we can rule out 779 = 19×41 because 19 is taken by K, which leaves 3ac = 221 = 13×17, so B = 17, D = 13 and A = 41.
For clue 6dn, 37(2E − F) must be one of the odd down entries {555, 777}, as 133 is already taken by 5dn, so 2E − F is one of {15, 21}. The unassigned primes are {11, 23, 31}, all 1 less than a multiple of 4; 21 is 1 greater than a multiple of 4, so F + 21 would always be a multiple of 4, making E = (F + 21)/2 an even number, not prime. Therefore E = (F + 15)/2 and is one of {13, 19, 23}, of which the only available prime is E = 23, with F = 31 and 6dn = 555. The only remaining prime is N = 11, which is a factor of 7dn = 1111.
