This is one possible solving path. There are 47 clues, so the highest possible clue number is 47 (if all the clue numbers are different), and both the across and the down clue numbers are increasing sequences in the range 1 to 47 inclusive.

From the down clue numbers, HO > SO, so H > S, ie H ≥ 2. From across clue numbers, YE > HE, so Y > H, ie Y ≥ 3. Clue number (SH)^Y is the 20th down clue, so it’s ≥ 20; it’s the 5th-to-last down clue, so it’s also ≤ 43. If Y is 3, the only cube in that range is 3³ = 27, but SH can’t be 3 if Y is 3. There are no 4th powers in the range [20, 43], so Y can’t be 4. For 5th powers there’s only 2⁵ = 32, and 2⁶ = 64 is too high, so Y can’t be 6 or greater. Therefore Y = 5, H = 2, S = 1 (so that SH = 2) and the clue number (SH)^Y = 32.

The US (= U) clue number is the 7th down clue and is 13 before clue 32, so U is in the range [7, 19]. By the same logic, clue number HUH (= 4U) is in the range [17, 29]. The only value that fits both is U = 7, giving clue numbers US = 7, HUH = 28 and YU = 35. Now we know the first seven down clues are numbered 1 to 7; in particular, 1 = H + U − E = 2 + 7 − E, so E = 8.

The two clues between 32 and 35 must be 33 = OR and 34 = P + O. To make 33, O and R must be {3, 11}, and clue number O − R is ≥ 8, so R = 3 and O = 11. To make 34 = P + O, P = 23. To make 2 = D − O, D = 13, and to make 3 = T − O − E, T = 22.

The across clue number RI is two after RY + E = 23 and three before T + O = 33, so 25 ≤ 3I ≤ 30, which limits I to {9, 10}. Down clue number S + I − N = 4, so N = I − 3, ie one of {6, 7}; but we already have U = 7, so N = 6 and I = 9. Across clue RI + SK is one after YE = 40 and two before R + YE = 43, so 41 = RI + SK = 27 + K, which makes K = 14.

Down clue number A + N is one of {30, 31}, so A is in {24, 25}, making across clue A − N one of {18, 19}. Clue number S + I + C is between that and UR = 21, so 10 + C is one of {19, 20}; C can’t be 9 because that’s I, so C = 10. Now down clue 5 = C + O − B = 21 − B, so B = 16. Down clue C + O − L = 21 − L is one of {9, 10}, so L is one of {11, 12}; but 11 is taken by O, so L = 12. Across clue 42 = F + O + B = F + 27, so F = 15.

Between across clues RO + Y = 38 and YE = 40, there’s only 39 = H + A + L = A + 14, so A = 25. Down clue 6 = A − M, so M = 19. Across clue number H + A − W = 27 − W is < 5, so W > 22 and the only available numbers are {24, 26} and the first clue is either 1ac or 3ac, with a value of SO^Y = 1×11⁵ = 161051. The value of 3dn is S/(AY) = 1/(25×5) = 0.008 (a finite, non-recurring decimal, so it doesn’t have to be entered in the form “1/125”), so the entry starts with 0, which means it can’t be the start of 3ac; thus the first clue is 1ac, ie 27 − W = 1, so W = 26.

We now have all the clue numbers except two across ones, G + 9 and G + 11, both in the range [28, 32], so G is in the range [19, 21]; 19 is taken by M, so G is one of {20, 21}. If G is 21 then 27ac = G/(E + N) = 21/14 = 1.5 (a finite decimal), but that would occupy only three cells, not four as the preamble stipulates. Therefore G = 20. The only unassigned numbers are now {4, 17, 18, 21, 24}. For 5ac = (Z + 8)⁶, (17 + 8)⁶ = 244140625 has nine digits, more than the maximum eight stipulated, so Z = 4.

For 31ac we have the value (G + R − E + N)ADA = 170625, so 31dn = PYX = 115X also has to start with 1. For X in {17, 18, 21, 24}, the corresponding values are {1955, 2070, 2415, 2760}, so X = 17.

There are 23 across clues and because of symmetry the 12th one, 25ac = 49.28 must go in the middle of the middle row of the grid. The entries before and after it must have the same length, being symmetrical opposites. They are 23ac = 22/165 or 2/15 (6 or 4 cells) and 27ac = 20/14 or 10/7 (5 or 4 cells); neither can be a finite decimal, being 0.1333333… and 1.4285714… respectively. To be the same length, they must be entered as 2/15 and 10/7.

We now have almost all the clue answers/entries, and from symmetry we know the lengths of the missing across ones: 1ac = 161051, 5ac = 2985984, 10ac = 406.125, 12ac = _____, 13ac = 1105, 15ac = 681503, 16ac = 56006721, 19ac = 24137569, 20ac = 738639, 21ac = 725760, 23ac = 2/15, 25ac = 49.28, 27ac = 10/7, 29ac = ______, 31ac = 170625, 33ac = 16777559, 37ac = 33534749, 38ac = 326592, 39ac = 1904, 40ac = 651.7, 41ac = 912.673, 42ac = _______, 43ac = 234256; 1dn = 1485172, 2dn = 161078, 3dn = 0.008, 4dn = 5156/343, 5dn = 25/243, 6dn = 83853, 7dn = 5.12, 8dn = 9150570, 9dn = 45369, 11dn = 161172, 14dn = 1729, 17dn = 266/23, 18dn = 23/169, 22dn = 287/3123, 24dn = 1679616, 26dn = ?, 28dn = 7529536, 30dn = 153/92, 31dn = 1955, 32dn = 607062, 33dn = 10368, 34dn = 70972, 35dn = 149.4, 36dn = 85.8.

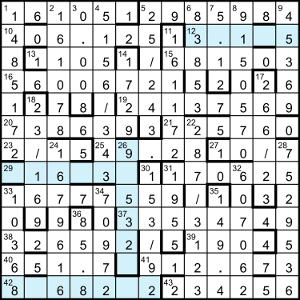
The grid has 13 columns, so the only way of fitting the 23 across answers into the 13 rows is to combine them in rows with entry lengths as follows: 6&7, 7&5, 4&6, 8, 8, 6&6, 4&5&4, 6&6, 8, 8, 6&4, 5&7, 7&6. Thus the top row is filled with 1ac = 161051 and 5ac = 2985984, which gives unique starting positions for down answers 2dn to 9dn, and the rest of the grid can be built up as shown here.

From this, we see that 42ac = 2V⁵ is in the range [8068202, 8968292], so V is between (8068202/2)^1/5 ≈ 20.9 and (8968292/2)^1/5 ≈ 21.4, ie V = 21, which makes 42ac = 8168202 and 29ac = 916839.

Now 26dn = 3J⁴ is 99532_, so J is between (995320/3)^1/4 ≈ 23.99995 and (995329/3)^1/4 ≈ 24.000006, ie J = 24 and 26dn = 995328. The only remaining variable is Q = 18, making 12ac = 3.125, and the grid is complete.