This is one possible solving path. Because numbers on opposite faces of the die are n and (7 − n), the triplet of digits for each position in the three grids must contain a 1 or 6, a 2 or 5 and a 3 or 4.

For the squares T7, F7 and R7, the only possible last digits are {1, 4, 5, 6}, so one of them ends in 5, another ends in 4 and the remaining one ends in 1 or 6. The first of those is (5n)² = 25n², so it ends in 25, and the other two squares can’t have 2 or 5 as their third digit. If it starts with 1, the square root is between √1125 ≈ 33.5 and √1625 ≈ 40.3 and the only number in that range ending in 5 is 35; starting with 2, the root is in the range [√2125 ≈ 46.1, √2625 ≈ 51.2], which contains no multiples of 5; for 3, [√3125 ≈ 55.9, √3625 ≈ 60.2] has no multiples of 5; for 4, [√4125 ≈ 64.2, √4625 ≈ 68.007] has only 65; for 5, [√5125 ≈ 71.6, √5625 = 75] has only 75; for 6, [√6125 ≈ 78.3, √6625 ≈ 81.4] has no multiples of 5; so the square ending in 5 is one of {35² = 1225, 65² = 4225, 75² = 5625}.

The square ending in 4 is a multiple of 4 (as it’s (2n)²), so its third digit must be even, ie it’s __44 or __64 (because 2 isn’t available) and its square root ends in 2 or 8. If it starts with 1 the root is in the range [√1144 ≈ 33.8, √1664 ≈ 40.8], which contains only 38 ending in 2 or 8; for 2, [√2144 ≈ 46.3, √2664 ≈ 51.6] has only 48 but 48² = 2304 isn’t allowed; for 3, [√3144 ≈ 56.1, √3664 ≈ 60.5] has only 58; for 4, [√4144 ≈ 64.4, √4664 ≈ 68.3] has only 68 but 68² = 4624 doesn’t end in 44 or 64; for 5, [√5144 ≈ 71.7, √5664 ≈ 75.3] has only 72 but 72² = 5184 isn’t allowed; for 6, [√6144 ≈ 78.4, √6664 ≈ 81.6] has no suitable values; so the square ending in 4 is one of {38² = 1444, 58² = 3364}.

If the 4-square is 3364 then the 5-square can’t be 4225 because their first digits 3 and 4 are on opposite faces of the die. If the 5-square is 1225 then the third square matches [25][16][34][16]; if it starts with 21 the bounds for the root are [√2131 ≈ 46.2, √2146 ≈ 46.3]; for 26 the bounds are [√2631 ≈ 51.3, √2646 ≈ 51.4]; for 51 the bounds are [√5131 ≈ 71.6, √5146 ≈ 71.7]; for 56 the bounds are [√5631 ≈ 75.04, √5646 ≈ 75.1]; but none of those ranges contains an integer.

If the 5-square is 5625 then the third square matches [16][25][34][16]; if it starts with 12 the bounds for the root are [√1231 ≈ 35.1, √1246 ≈ 35.3]; for 15 the bounds are [√1531 ≈ 39.1, √1546 ≈ 39.3]; for 62 the bounds are [√6231 ≈ 78.9, √6246 ≈ 79.03]; for 65 the bounds are [√6531 ≈ 80.8, √6546 ≈ 80.9]; the only integer in those ranges is 79, giving 79² = 6241. To fit the first digits of the three squares {3364, 5625, 6241} onto the die shown in the preamble, in top-front-right order they could be 3-6-5 (or 6-5-3 or 5-3-6), but then the corresponding third digits 6-4-2 (or 4-2-6 or 2-6-4) don’t fit on the die, because with 6 on top and 4 on the front, the right face is 5. Therefore, with 3364 there’s no possible value for the 5-square, so the 4-square is 1444.

Now the 5-square is in {4225, 5625}, because it can’t have the same first digit as the 4-square. If it’s 5625 then the third square matches [34][25][16][16]. Its root ends in one of {1, 4, 6, 9} and is bounded by [√3211 ≈ 56.7, √4566 ≈ 67.6]; there are four such integers, whose squares are {59² = 3481, 61² = 3721, 64² = 4096, 66² = 4356}. The first three all contain invalid digits and 4356’s third digit is incompatible with that of 5625 (because 2 and 5 are on opposite faces). Therefore the 5-square is 4225.

From the die’s orientation, if we put 4225 on top and 1444 on the front then the right face will show 5661, not a square; if we switch them, the right face has 2116 = 46². So, in top-front-right order the squares are {1444, 4225, 2116}, {4225, 2116, 1444} or {2116, 1444, 4225}.

Whichever order they’re in, they have a digit sum of 36, and the rest of the cells can’t contain more than 12×(4 + 5 + 6) = 180, so the total digit sum is ≤ 196. If X is 5 then the maximum for F3 is 5×196 = 980, too small; therefore X = 6 and F3 ≤ 6×196 = 1176. Both T3 and F3 have a factor of X = 6 and are thus even, so the square with an odd third digit has to go at R7 = 2116, which places T7 = 1444 and F7 = 4225. Now F3 = 11_2 and to be a multiple of 6 it’s one of {1122, 1152}.

F4 now ends in 5, so it’s a power of a number ending in 5. 25³ = 15625 is too big; the only four-digit power of 15 is 15³ = 3375, with an invalid digit; the only four-digit power of 5 is 5⁵ = 3125, so F4 = 3125. In the Front grid we need Y occurrences of Y, which can’t be 1 or 2 because there are now three of each already. It also can’t be 6 (that’s X) or 5, because that would make T2 and T3, multiples of 6Y, end in 0. So Y is in {3, 4}.

T1dn ends in 1, so it’s a power of a number ending in {1, 3, 7, 9}. The only such four-digit powers are {3⁸ = 6561, 7⁴ = 2401, 9⁴ = 6561, 11³ = 1331, 21³ = 9261}; eliminating the ones with invalid digits leaves {1331, 6561}. If T1dn is 1331, then all six occurrences of X = 6 are forced, because they can’t go in the cells where there’s a 1 in the Front grid. Then T1ac = n² − Y² ends in 6, with Y² = 9 (because Y² = 16 would make n² end in 2, not a square). The square root would be bounded by [√1616 ≈ 40.2, √1656 ≈ 40.7] but there are no integers in that range. Therefore T1dn = 6561.

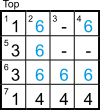
Now T1ac is 6_[2345]_, so the square n² is bounded by [6121 + 3² = 6130, 6656 + 4² = 6672], with the root between √6130 ≈ 78.3 and √6672 ≈ 81.7, ie n is in {79, 80, 81}. It can’t be 80 because 6400 − 9 = 6391 and 6400 − 16 = 6384 have invalid digits; that leaves {6232, 6225, 6552, 6545} as the possibilities for T1ac. But now there are only four possible places in the Top grid for the four more 6s we need to enter, which completes T6 = 6666.

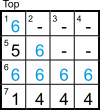
The T6 clue tells us that IOA’s age is a factor of 6666 = 2×3×11×101. Also, the square of the age is R5 + W. None of the second to fourth digits of R5 can be 1 or 6 because in those cells we have a 6 in the Top grid and 1s in the Front. So R5 + W is in the range [1222 + 1 = 1223, 6555 + 5 = 6560] and the age is bounded by [√1223 ≈ 34.97, √6560 ≈ 80.99]; the only factor of 6666 in that range is age = 66, so R5 is in [66² − 4 = 4352, 66² − 1 = 4355] (not 4351 because we’re not allowed a 1) and we can enter the 435.

For the first digit of 5ac, we have Top = 5 and Right = 4, so to fit on the die we must have Front = 6. For the second digit, Top = 6 and Right = 3, make Front = 5, completing F5 = 6511. For the third digit, Front = 1 and Right = 5, make Top = 4. Similarly, for the last digit of 6ac, Top = 6 and Front = 2 make Right = 4.

For T3 we have [2345]464 and it’s a multiple of 6Y; the only multiple of 3 is T3 = 4464, which eliminates all the possibilities for T1ac except T1ac = 6545, with Y = 4. For the third digit of 1ac, Top = 4 and Front = 1 make Right = 5; for the fourth digit, Top = 5 and Front = 3 make Right = 6.

The Top grid is now complete apart from the last digit of 5ac, which is one of {2, 3, 4, 5}. It has a maximum of four 5s, one 3 and one 2, so W can’t be any of those, ie W = 1 (and there’s exactly one 1 in the Top grid). That makes R5 = 4355, and its last digit of Right = 5 and Front = 1 make Top = 4, completing the Top grid.

R2 ends in 1 and it’s a multiple of (6 + Z), so Z is odd, one of {3, 5}. For F1dn = n² + 4Z we have _6_4. If Z is 3 then n² = _6_4 − 12 ends in 2, not a square; therefore Z = 5.

In the Front grid we need three more 4s (Ys) in the remaining four available places, so at least one of the unknown digits in F1dn = n² + 20 is 4. If it doesn’t start with 4 then n² is one of {2644 − 20 = 2624, 3644 − 20 = 3624, 5644 − 20 = 5624}, none of which is a square, so it does start with 4. Of the four possibilities for the third digit, only F1dn = 4644 works, being 68² + 20. Knowing all the digits for 1dn in the Top and Front grids, we can use the die to complete R1dn = 5452. Now exactly one of the two unknown digits in F2 is a 4. It can’t be the third digit because that would make the corresponding Right digit a 5, but we already have a full complement of five 5s there. So 4 is at the start of F2, completing F1ac = 4413 and making R1ac = 5156.

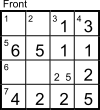
Now R2 is a multiple of 11 matching 13_1, for which only R2 = 1331 = 11×121 works. Using the die, that makes F2 = 4552.

F3 is one of {1122, 1152}. If the third digit is 5, the die makes the corresponding in the Right grid 3; then the sum of all digits is 189, but 189×6 = 1134 doesn’t match 1152 for F3. So the third digit must be 2, with 4 in the Right grid, a digit sum of 187, and 187×6 agrees with F3 = 1122. The grids are complete.